索引及底层数据结构详解

索引

索引的本质

索引是帮助MySQL高效获取数据的排好序的数据结构。

查询SQL

/**
  查询 col2 = 89 的数据
 */
select * from example_table where col2 = 89;

初始化表SQL

/**
  引用下面SQL在库中创建二叉树数据结构临时表
 */
CREATE TABLE `example_table`  (
  `id` int NOT NULL AUTO_INCREMENT COMMENT '主键',
  `col1` int NULL DEFAULT NULL COMMENT 'Col1',
  `col2` int NULL DEFAULT NULL COMMENT 'Col2',
  PRIMARY KEY (`id`) USING BTREE
) ENGINE = InnoDB CHARACTER SET = utf8mb4 COLLATE = utf8mb4_unicode_ci COMMENT = '二叉树数据结构临时表' ROW_FORMAT = Dynamic;

初始化数据SQL

/**
  插入数据
 */
INSERT INTO `example_table` (`col1`, `col2`) VALUES (1, 34);
INSERT INTO `example_table` (`col1`, `col2`) VALUES (2, 77);
INSERT INTO `example_table` (`col1`, `col2`) VALUES (3, 5);
INSERT INTO `example_table` (`col1`, `col2`) VALUES (4, 91);
INSERT INTO `example_table` (`col1`, `col2`) VALUES (5, 22);
INSERT INTO `example_table` (`col1`, `col2`) VALUES (6, 89);
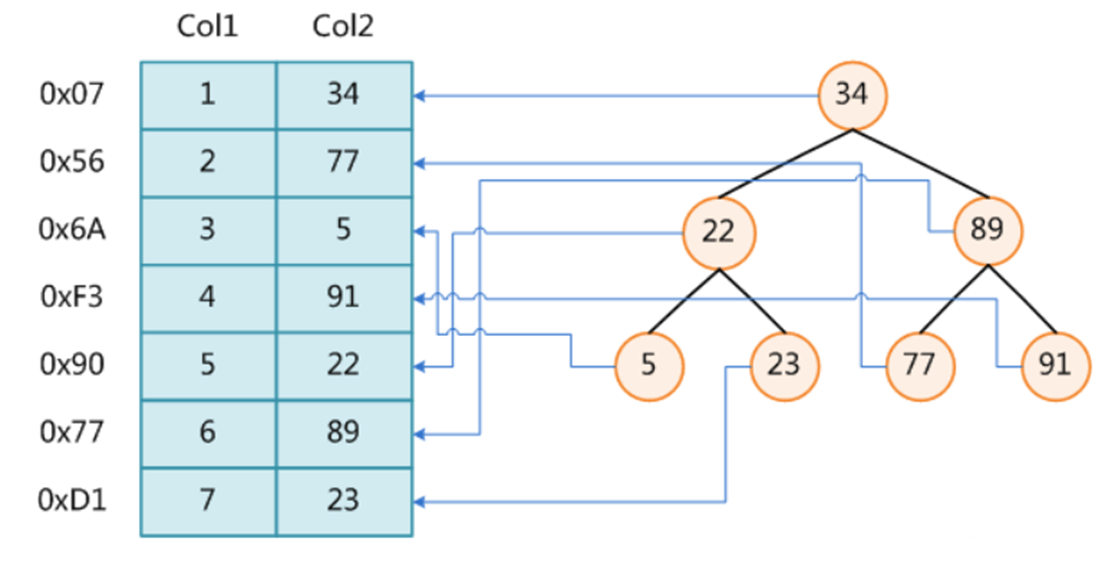
INSERT INTO `example_table` (`col1`, `col2`) VALUES (7, 23);

假设每次从磁盘拿取一条数据，当没有在col2列创建索引时，需要从第一条数据开始遍历，直至找到col2=89的数据为止，需要6次I/O交互。

从磁盘中拿取数据需要与磁盘做I/O交互，在没有索引的情况下，需要在磁盘中逐条数据读取，然后在程序中通过CPU进行比对，查看是否符合查询条件。明显，这样的效率是不高的。

因此提高查询效率的关键之一就是减少与磁盘交互的I/O次数，如果将次数控制在一定的范围内，则效率会有明显提升，这也是数据结构的明显作用。

数据在硬盘中的存储

数据表中的数据在电脑磁盘(硬盘)中是随机分布的，并不一定是紧邻的。

比如我第一天往表里插入 id = 1 的记录，过了几天才插入了 id = 2 的记录，而磁盘写入数据是一个磁道一个磁道去写入，因此他们的实际存储位置可能不是紧邻的，插入 id = 2 的数据之前，可能早已有其他程序已经把 id = 1 的数据所在磁盘位置的周围都写满了。

聚集索引

聚集索引（Clustered Index）是一种特殊的索引结构，直接决定了表中数据行的物理存储顺序。它的核心特点是：索引的叶子节点存储的是完整的数据行，而非指向数据的指针。与非聚集索引（Secondary Index）相比，聚集索引与数据存储的物理结构深度绑定。

核心特性

• 数据行与索引绑定
  聚集索引的叶子结点存储的是完整的数据行（而非指针）
  • 表中的数据行在磁盘上按聚集索引的键值顺序存储
  • 每张表有且仅有一个聚集索引（因为数据行只能按一种物理顺序存储）
• 主键即聚集索引 在 Innodb 中，聚集索引默认由主键（Primary key）定义：
  • 如果表定义了主键，则主键自动成为聚集索引
  • 如果未定义主键，Innodb 会选择一个唯一的非空索引（Unique Not Null）作为聚集索引
  • 如果没有符合条件的索引，Innodb 会隐式生成一个 6 字节的 RowID 作为聚集索引
• 查询效率优势
  • 通过聚集索引访问数据时，无需二次查找（回表），可直接从索引的叶子结点获取完整的数据行

聚集索引优势

• 主键查询极快
  直接通过聚集索引定位到数据行，无需额外查找

  select * from students where id = 3; // 直接命中聚集索引

• 范围查询高效
  数据按主键顺序存储，范围查询（如 id > 100）可以快速定位连续的磁盘块，减少随机 I/O
• 覆盖索引优化
  如果查询只需主键列，无需访问数据行（例如 COUNT(*)）

聚集索引劣势

• 插入可能引发页分裂
  如果主键是随机值（如 UUID），新插入的数据可能导致数据页分裂，降低写入性能
• 更新主键代价高
  修改主键值会导致数据行物理位置的移动，影响性能

问题汇总

为什么建议InnoDB表必须建主键，并且推荐使用整型的自增主键？

• 建议建主键
  • 如果未显示定义主键，Innodb 会按照以下规则寻找或创建主键
    • 找唯一非空索引：从第一列开始逐列检查，选择一个所有值唯一的列的作为主键
    • 隐式生成隐藏列：若没有符合条件的列，Innodb 会自动生成一个 6字节的隐藏 ROWID 列作为主键
  • 浪费资源
    • 隐式生成的主键会消耗额外存储空间和计算资源，且可能影响性能（如索引效率低）
• 使用整型
  • 比较效率高
    整型（如INT）的比较操作比字符串快（如UUID）快
    • 整数 100 和 200 的比较直接通过数值大小判断
    • 字符串 "abc" 和 "abd" 需要逐个字符按照 ASCII 码对比，耗时更长
  • 存储空间少
    整型占用更少空间（如INT占4字节，BIGINT占8字节），而UUID字符串通常需要36字节。若表有100万条记录，使用INT主键比UUID节省约32MB空间
    • 使用整型主键，B+树中每个节点能存储更多键值，减少内存和磁盘I/O开销
    • 非聚集索引的叶子节点存储的是主键值。若主键为整型，非聚集索引的存储空间更小，查询效率更高。
• 推荐自增
  • 减少页分裂
    • 页分裂的代价
      Innodb的数据页（默认16kb）按B+树结构存储。当插入非自增的主键（如UUID或时间戳）时，新数据可能插入到中间的页，导致：
      • 页分裂：当页满时，需将数据拆分到新页，引发额外的I/O和CPU开销
      • 碎片增多：频繁分裂导致数据页不连续，降低读取效率
    • 自增主键的优势
      自增主键保证数据按顺序插入到B+树的末尾，无需频繁页分裂，减少磁盘碎片，提升写入性能
  • 优化I/O
    • 顺序写入的高效性
      自增主键的数据写入是顺序的，可利用磁盘的顺序读写特性，减少随机I/O的等待时间
    • 缓存命中率高
      顺序数据更容易被缓存（如Innodb Buffer Pool）,减少磁盘访问次数

非聚集索引

非聚集索引（Non-Clustered Index）是一种独立于数据物理存储结构的索引类型。它的核心特点是：索引的叶子节点不存储完整的数据行，而是存储主键值（或行指针），通过主键值再到聚集索引中查找完整数据行（这一过程称为 回表）。非聚集索引与聚集索引共同构成了数据库的索引体系。

核心特性

• 索引与数据分离 非聚集索引的叶子节点存储的是 主键值（或行指针），而非完整数据行。
• 可创建多个非聚集索引 每张表可以有多个非聚集索引（例如，为多个高频查询字段分别建立索引）。
• 索引本身有序 非聚集索引的键值按索引列的顺序排序，但 数据行的物理存储顺序与索引无关。

非聚集索引优势

• 支持多索引，灵活优化查询
  多字段索引：允许为不同的查询条件创建多个索引，例如为 email、phone 或 name 分别建立索引

  create index idx_email on user(email);
  create index idx_phone on user(phone);

• 覆盖索引减少回表
  若查询字段全部包含在索引中，无需回表，直接从索引获取数据
• 加速排序和分组操作 排序优化：索引本身有序，可避免全表排序

非聚集索引劣势

• 回表带来的性能损耗

  select name, email from user where name = 'Alice';

  • 通过 name 索引找到主键值
  • 通过主键值回表，在聚集索引中使用主键值查询对应的叶子结点数据，返回叶子结点包含的 email 字段值
• 索引维护成本高
  • 写入开销 每次插入、更新或删除数据时，需同步更新所有相关索引。表含 5 个非聚集索引 → 每次写入需修改 5 个索引结构。
  • 影响 高并发写入场景下，可能成为性能瓶颈

问题汇总

非聚簇索引的叶子结点为什么存储主键值而不是整行数据呢？

非聚集索引的叶子节点存储主键值，是为了在一致性、维护成本之间取得平衡

• 一致性
  主键值稳定，避免因数据物理位置变化导致的索引失效。
• 维护成本
  仅需维护聚集索引的物理结构，非聚集索引无需频繁更新，而且也能节省更多的存储空间。
• 扩展性
  支持多非聚集索引，且通过统一的主键定位机制简化设计。

联合索引

存储引擎

MYISAM

INNODB

Memory

数据结构

推荐数据结构网址，可在其中了解各类数据结构的存储方式
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

二叉树

特点

• 对半搜索,每个节点最多两个子节点
• 若左子树不空，则左子树上所有节点的值都小于根节点的值；
• 若右子树不空，则右子树上所有节点的值都大于根节点的值；
• 任意节点的子树也都是二叉排序树(二叉搜索树)；
• 二叉排序树的查找性能在$O(lo{g}_{2}n)$ - $O(n)$,其中$n$是节点数量。

如上图所示，如果在col2列上使用二叉树结构建立一个索引，key为col2列的值，value为对应行数据所在的磁盘文件地址，则从根节点去查找，只需要两次I/O交互，即可查询到指定数据。

但MySQL没有选择二叉树作为索引结构，因为二叉排序树并不会进行任何维护平衡的操作，如果连续插入已排好序的数据，这将可能会退化成链表结构，最坏的情况下，查找、插入和删除的时间复杂度将退化为$O(n)$。

二叉树插入顺序增长数据动态图

红黑树

红黑树（Red-Black Tree）是一种自平衡的二叉搜索树（BST），通过在插入和删除时调整结构来保持近似平衡，从而避免与普通二叉树一样，在 key 在已排好序的情况下进行插入而导致树结构退化为链表结构。它保证了最坏情况下的时间复杂度为 $O(lo{g}_{2}n)$，被广泛应用于各类编程语言的库实现中（如Java的TreeMap）。

特点

红黑树必须满足以下5条性质：

• 颜色属性：每个节点是红色或黑色。
• 根属性：根节点必须是黑色。
• 叶子属性：所有叶子节点（NIL节点，空节点）是黑色。
• 红色节点规则：红色节点的两个子节点必须都是黑色（即不能有连续的红色节点）。
• 路径属性：从任意节点到其所有叶子节点的路径上，黑色节点的数量相同。

📌 黑高（Black Height）：从节点到叶子节点的路径上的黑色节点数量，是红黑树平衡的关键指标。

节点插入操作

1. 标准BST插入：将新节点插入到合适的位置，并初始化为红色。
2. 修复红黑树性质：根据父节点和叔节点的颜色进行调整：
   • Case 1：叔节点是红色
     → 将父节点和叔节点变黑，祖父节点变红，然后递归处理祖父节点。
   • Case 2：叔节点是黑色，且新节点是父节点的右子（或左子）
     → 对父节点左旋（或右旋），转化为Case 3。
   • Case 3：叔节点是黑色，且新节点是父节点的左子（或右子）
     → 父节点变黑，祖父节点变红，然后对祖父节点右旋（或左旋）。

📌 左旋：当对一个节点执行左旋时，该节点的右子节点将成为新的父节点，而原来的节点则成为其新父节点的左子节点。此操作不会改变旋转节点的右子节点的右子树，但会将右子节点的左子树变为原节点的右子树。
📌 右旋：右旋与左旋相反，当对一个节点执行右旋时，该节点的左子节点将成为新的父节点，而原来的节点则成为其新父节点的右子节点。此操作不会改变旋转节点的左子节点的左子树，但会将左子节点的右子树变为原节点的左子树。

节点删除算法

1. 标准二叉搜索树删除

   1. 无子节点：直接删除。

   2. 一个子节点：用子节点替代被删除节点。

   3. 两个子节点：找到后继节点替换值，递归删除后继节点。

2. 删除后调整

   1. 若被删节点为红色：无需调整。

   2. 若被删节点为黑色：需通过旋转和颜色调整恢复平衡：

具体插入删除Java代码

enum Color { RED, BLACK }

class RBNode<T extends Comparable<T>> {
    T data;
    Color color;
    RBNode<T> parent, left, right;

    public RBNode(T data) {
        this.data = data;
        this.color = Color.RED; // 新节点默认红色
        this.parent = this.left = this.right = null;
    }
}

public class RedBlackTree<T extends Comparable<T>> {
    private RBNode<T> root;
    private final RBNode<T> NIL = new RBNode<>(null); // 虚拟NIL节点（黑色）

    public RedBlackTree() {
        NIL.color = Color.BLACK;
        root = NIL;
    }

    // 插入入口
    public void insert(T data) {
        RBNode<T> newNode = new RBNode<>(data);
        newNode.left = newNode.right = NIL;
        insertBST(newNode);
        fixInsert(newNode);
    }

    // 二叉搜索树插入
    private void insertBST(RBNode<T> node) {
        RBNode<T> current = root;
        RBNode<T> parent = null;

        while (current != NIL) {
            parent = current;
            if (node.data.compareTo(current.data) < 0) {
                current = current.left;
            } else {
                current = current.right;
            }
        }

        node.parent = parent;
        if (parent == null) {
            root = node;
        } else if (node.data.compareTo(parent.data) < 0) {
            parent.left = node;
        } else {
            parent.right = node;
        }
    }

    // 插入后修复
    private void fixInsert(RBNode<T> node) {
        while (node != root && node.parent.color == Color.RED) {
            RBNode<T> uncle;
            if (node.parent == node.parent.parent.left) {
                uncle = node.parent.parent.right;
                if (uncle.color == Color.RED) { // Case 1: 叔红
                    node.parent.color = Color.BLACK;
                    uncle.color = Color.BLACK;
                    node.parent.parent.color = Color.RED;
                    node = node.parent.parent;
                } else {
                    if (node == node.parent.right) { // Case 2: LR型
                        node = node.parent;
                        leftRotate(node);
                    }
                    // Case 3: LL型
                    node.parent.color = Color.BLACK;
                    node.parent.parent.color = Color.RED;
                    rightRotate(node.parent.parent);
                }
            } else { // 对称处理右子树
                uncle = node.parent.parent.left;
                if (uncle.color == Color.RED) {
                    node.parent.color = Color.BLACK;
                    uncle.color = Color.BLACK;
                    node.parent.parent.color = Color.RED;
                    node = node.parent.parent;
                } else {
                    if (node == node.parent.left) { // Case 2: RL型
                        node = node.parent;
                        rightRotate(node);
                    }
                    // Case 3: RR型
                    node.parent.color = Color.BLACK;
                    node.parent.parent.color = Color.RED;
                    leftRotate(node.parent.parent);
                }
            }
        }
        root.color = Color.BLACK; // 确保根节点为黑
    }

    // 左旋
    private void leftRotate(RBNode<T> x) {
        RBNode<T> y = x.right;
        x.right = y.left;
        if (y.left != NIL) y.left.parent = x;
        y.parent = x.parent;
        if (x.parent == null) {
            root = y;
        } else if (x == x.parent.left) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
        y.left = x;
        x.parent = y;
    }

    // 右旋（对称）
    private void rightRotate(RBNode<T> x) {
        RBNode<T> y = x.left;
        x.left = y.right;
        if (y.right != NIL) y.right.parent = x;
        y.parent = x.parent;
        if (x.parent == null) {
            root = y;
        } else if (x == x.parent.right) {
            x.parent.right = y;
        } else {
            x.parent.left = y;
        }
        y.right = x;
        x.parent = y;
    }

    public static void main(String[] args) {
        RedBlackTree<Integer> tree = new RedBlackTree<>();
        tree.insert(10);
        tree.insert(20);
        tree.insert(5);
        tree.insert(15);
        // 插入后自动平衡
        System.out.println(tree.root);
    }
    
}

MySQL也没选择红黑树作为索引的存储结构。
因为随着数据量的增长，树的高度也会无限制的增长,并没有从根本上将输的高度控制在一定范围之内。
根本上的解决方式还是将树的高度固定在一定的高度内，减少磁盘的I/O次数。

Hash表

特点

• 对索引的key进行一次hash计算就可以定位出数据存储的位置。
• 很多时候Hash索引要比B+树索引更高效
• 仅能满足“=”、“IN”，不支持范围查询
• hash冲突问题

B-Tree

特点

• 叶节点具有相同的深度
• 叶节点的指针为空
• 所有索引元素不重复
• 节点中的数据索引从左到右递增排列

B+Tree

特点

• 非叶子结点不存储data，只存储索引（冗余），可以放更多的索引。
• 叶子结点包含所有索引字段。
• 叶子结点用指针连接，提高区间的访问性能。